

Some basic theorems about similar triangles are: The corresponding sides of similar triangles have lengths that are in the same proportion, and this property is also sufficient to establish similarity. Two triangles are said to be similar, if every angle of one triangle has the same measure as the corresponding angle in the other triangle. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is 360 degrees. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it this is the exterior angle theorem. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. This allows determination of the measure of the third angle of any triangle, given the measure of two angles. This fact is equivalent to Euclid's parallel postulate. The sum of the measures of the interior angles of a triangle in Euclidean space is always 180 degrees. The measures of the interior angles of the triangle always add up to 180 degrees (same color to point out they are equal). Elementary facts about triangles were presented by Euclid, in books 1–4 of his Elements, written around 300 BC. In rigorous treatments, a triangle is therefore called a 2- simplex (see also Polytope). Triangles are assumed to be two- dimensional plane figures, unless the context provides otherwise (see § Non-planar triangles, below). A triangle with vertices A, B, and C is denoted △ A B C īasic facts A triangle, showing exterior angle d. Before we dive into the in-depth definition, a scalene triangle is a triangle that has no equal sides. An isosceles triangle is a triangle that has two equal sides and two equal angles. It is one of the basic shapes in geometry. A triangle is called an equilateral triangle if all three of its sides are equal and its angles are equal as well (60 each). You also should now see the connection between the Isosceles Triangle Theorem to the Side Side Side Postulate and the Angle Angle Side Theorem.A triangle is a polygon with three edges and three vertices. The converse of the isosceles triangle theorem is true! Lesson summaryīy working through these exercises, you now are able to recognize and draw an isosceles triangle, mathematically prove congruent isosceles triangles using the isosceles triangles theorem, and mathematically prove the converse of the Isosceles Triangles Theorem. With the triangles themselves proved congruent, their corresponding parts are congruent (CPCTC), which makes BE ≅ BR. The Angle-Angle-Side Theorem states that If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent. That would be the Angle-Angle-Side Theorem (AAS). Let's see…that's an angle, another angle, and a side. Since line segment BA is used in both smaller right triangles, it is congruent to itself.
Since line segment BA is an angle bisector, this makes ∠EBA ≅ ∠RBA. Now we have two small, right triangles where once we had one big, isosceles triangle: △BEA and △BAR. Where the angle bisector intersects base ER, label it Point A. Given that ∠BER ≅ ∠BRE, we must prove that BE ≅ BR.Īdd the angle bisector from ∠EBR down to base ER. To prove the converse, let's construct another isosceles triangle, △BER. Unless the bears bring honeypots to share with you, the converse is unlikely ever to happen. If I attract bears, then I will have honey. The way that the term isosceles triangle is used in the Elements does not exclude equilateral triangles. The term isosceles triangle is first used in proposition I.5 and later in Books II and IV. If I have honey, then I will attract bears. According to this definition, an equilateral triangle is not to be considered as an isosceles triangle. If I lie down and remain still, then I will see a bear.įor that converse statement to be true, sleeping in your bed would become a bizarre experience. If I see a bear, then I will lie down and remain still. If the premise is true, then the converse could be true or false:
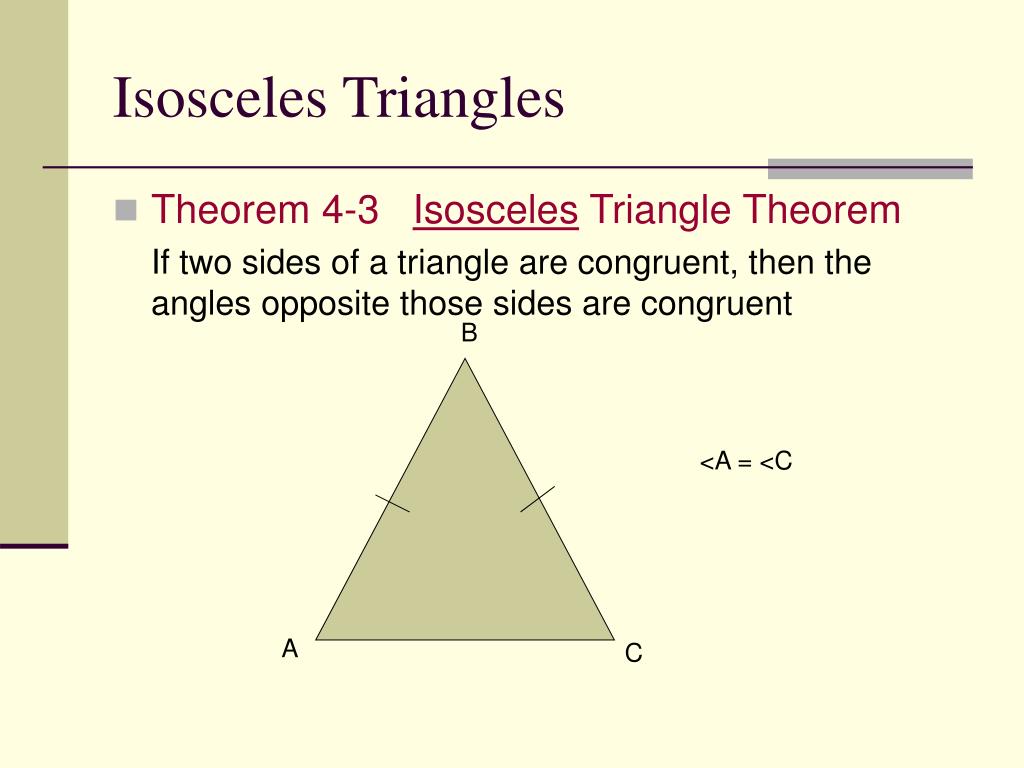
If the original conditional statement is false, then the converse will also be false. Now it makes sense, but is it true? Not every converse statement of a conditional statement is true. Converse Of the Isosceles Triangle Theorem


 0 kommentar(er)
0 kommentar(er)
